Hash Tables are one of the most used Data structures, they’re so popular that almost every language has their own implementation and nomenclature of Hash Tables.
One very interesting fact about Hash Tables is that they’re also used as building blocks for:
- Classes and its members
- Variable lookup table
As we can see, Hash Tables are not just used in the business case of any application, but it’s also used in the inner working of any programming language.
But what are Hash Tables exactly?
Hash Table are used to store Key-Value pairs. The defining features of a Hash Table are:
- Constant insertion
- Constant deletion
- Constant lookup
These constant time use cases are the reason why programming languages work so efficiently.
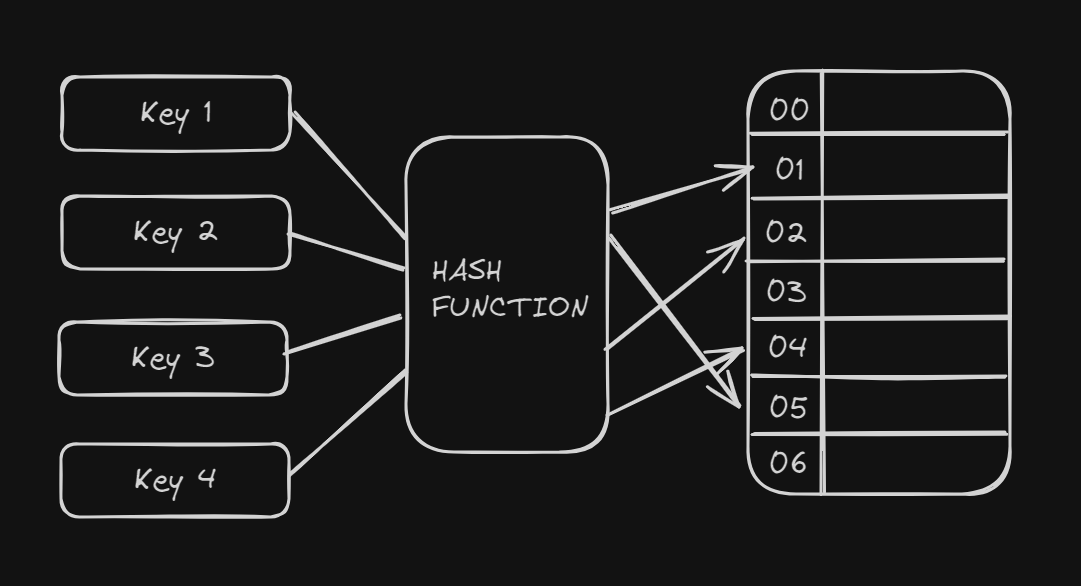
Hash Table working in simple terms
Application keys to hash keys
There is a particular set of data types which can be put as keys to a Hash Table, eg. string, int, tuple, etc. But obviously any language won’t want to restrict the number of types supported for accessing a Hash Table, so most languages provide a hash function to convert a custom type so that it can be used in a Hash Table. If you want to use a User Defined Class, you just have to create a Hash function inside your class which returns an integer and then the Hash Table can infer the hashing logic from your class and then do the heavy-lifting for you. Isn’t that great!
Naive implementation
If you already have a way to map an application key to an integer, you can use the integer as the index of an array to store the key value pairs.
We get constant time insertion, update and lookup, isn’t that great? NO. Although it looks good on paper performance wise but it works only when the N is very small. When the size of the number of keys increases, the size of array required will grow exponentially.So this implementation would have the following challenges:
- Finding a big chunk of memory is tough.
- Lots of slots would remain empty.
Mapping the hash key to a smaller range
The basic idea is that we should only allocate enough memory to the Hash Table so that it can store only that number of keys which are required. Not more.
This method saves a lot of memory, for example they hashing function can generate any int32 number and we just need to store 8 keys, this would have earlier needed 2 ^ 32 number of slots. But after mapping to a smaller range, we would only require 8 keys
But what if I need to more keys at a later stage?
The holding array would need to be resized. NOTE: This doesn’t mean we need to change the Hashing function, as it already was converting to int32 values(2 ^ 32 keys possible).
Why are we even hashing a complex data type key to int in the first place?
- Simplifying the problem statement of a Hash Table.
- Providing a good abstraction to implement Hash Table, i.e. the working of the Hash function doesn’t need to know the exact working of the Hashed key.
This enables the Hash Table to support Complex User defined data types.
Conflicts in Hash Tables
There would inevitably be cases where there would be multiple keys which can produce the same keys upon hashing. But we can’t delete the previous key and store a new one as it would make the Hash Table lossy and the user won’t want that. Then How to store multiple keys in the same slot? There are 2 classical ways to achieve this:
- Chaining: Form a chain of keys that hash to the same slot using a data structure(Linked Lists or Trees).
- Open Addressing: Instead of using some auxiliary data structure, use the empty slots.
Chaining
We put colliding keys to a data structure which holds the data well.
Most common implementation: Linked Lists
Chaining with linked lists
The core set of operations we need are:
- add a new key to the linked list
- check if the key is is present in the list
- remove a key from the list
Each slot of the array contains the pointer of the head of the linked list contains:
- pointer to the actual key
- pointer to the next node of the list
struct node{
void *key;
struct node *next;
}
Hash Table operations
1. Adding a key
Given a key and a value, we
- pass the key through the hash function and get index i
- create a new linked list node with key, value
- add it to the chain present at index i
Possible implementations
- Insertions always happen at the head.(fast)
- insertions always happens t the tail.(fast)
- insertions happen as per the sort order.(linear iteration, slow)
2. Deleting a key
Deleting a key is very straightforward:
- reach the slot in O(1 )
- iterate through the list and find the node with
node -> key == k1
- while iterating keep track of the previous node
- adjust the pointers
- delete the intended node
3. Lookup a key
Lookups are similar to delete:
- reach the slot in O(1)
- linearly iterate through the list until we findNOTE: When the collision increase for a particular key, it is best to resize the array than to use chaining.
node -> key == k
Other data structures for chaining:
Instead of linked lists, we can use self-balancing binary trees to store key, value pairs.
In this case insertions are not O(1), but lookups are O(n).
We can use Search Trees when we’re expecting large number of collisions (in cases where the array can’t be expanded so the keys would have to collide)
Open Addressing
When key collide, find a way to hunt for an available slot in the array, deterministically.
Deterministically here means that we can’t just randomly assign slots to colliding keys, as that would lead to linear lookup times.
The process of finding out a suitable slot for a colliding key is called probing.
Probing function
A good probing function should generate the permutation of the range (0, m - 1) so as to cover the entire space eventually.
Linear Probing
We search linearly from the hashed index until the end of the array then wrap from the start.
- We invoke the probing function to get the slot
- If key is present at that index, we
return- If not, we traverse to the right and try to find the key
- If we encounter the key, we
return- If we reach the end, we start from index 0
- We stop the iteration as soon as we encounter an empty slot
WORST CASE: Linear lookup across table
In Linear probing, deleting has to be done using soft delete, because if we do hard delete, it would create an empty slot, which means the probing key would never move forward for that colliding key of that same index.
Linear probing is simple and fast
Simple: We linearly iterate to find the next slot, can this BE any easier? Fast: Usage of Localized access i.e. the page is cached on CPU and the page contains the neighboring elements. So subsequent accesses are served on CPU cache.
But how can linear probing give constant time performance?
Because in an average case, there would be far fewer collisions. The keys would be distributed across your entire space.
Challenges with Linear probing
A bad hash function would make linear probing a few hash table search and hence inefficient. Hence, using a good hash function is very important, MurmurHash is preferred
Linear probing suffers from clustered collisions. To tackle this, a good uniform hash function is essential for linear probing to be efficient.
Quadratic Probing
Instead of placing the collided key in the neighboring slot, quadratic probing adds successive value of an arbitrary quadratic polynomial.
How is it better than linear probing?
It reduces clustering and cascaded collisions as collided keys are placed further away from each other. Note: It is not immune to it, it just reduces it a great extent.
It has a good locality of reference but not as great as linear probing Note: Leverages CPU cache well. So unless there are large collisions on same key, at least a couple of subsequent slots will be in CPU cache.
Now that we discussed the 2 most popular probing techniques and how they function, but can we do better?
The one thing which the above discussed probing techniques suffer is the clustering and cascaded collisions.
Conflict Resolution using Double Hashing
Double Hashing incorporates 2 hash functions to find the slot.
First hash function gives primary slot and upon collision, it uses second hash function as offset times attempt until an empty slot is reached.
Given that we’re using another hash function to find offset, we are minimizing repeated collisions and effects of clustering.
Choosing the second hash function
- It should never return 0.
- It should cycle through entire table(order does not matter)
- Fast to compute and should be nearly similar to a random number generator(in terms of uniformity).
Advantages of Double hashing
- Uniform spread upon collision.
- Follows no specific offset pattern (purely depends on the key).
- Least prone to clustering problem. (offset from primary slot is uniformly distributed)
I hope you liked reading this article. I’ll try to cover the Hash Table Performance and Implementation in the next blog.